APROXIMACIÓN Y ERRORES DE REDONDEO
Definiciones de error
Los errores numéricos se generan con el uso de aproximaciones para representar las operaciones y cantidades matemáticas. Estos incluyen errores de truncamiento, que resultan de representar aproximadamente un procedimiento matemático exacto, y los errores de redondeo, que resultan de representar aproximadamente números exactos.
- Errores de redondeo: Este tipo de errores se deben a que las computadoras solo guardan un numero finito de cifras significativas durante un cálculo.
- Errores de truncamiento: Los errores de truncamiento son aquellos que resultan al usar una aproximación en lugar de un procedimiento matemático exacto.
Cifras significativas
También es conocido como dígitos significativos y se ha desarrollado para designar formalmente la confiabilidad de un valor numérico. Él numero de cifras significativas es él numero de dígitos más un dígito estimado que se pueda usar con confianza. Por ejemplo:
8632574 redondeado a (4cs) es 8633000
3,1415926 redondeado a (5d) es 3,14159
1,6750 redondeado a (2d) es 1,68
Los ceros no son siempre cifras significativas ya que pueden usarse solo para ubicar el punto decimal.
El concepto de cifras significativas tiene dos implicaciones importantes en el estudio de los métodos numéricos.
1. Los métodos numéricos obtienen resultados aproximados, se deben desarrollar criterios para especificar que tan precisos son los resultados obtenidos. Una manera de hacerlo es en términos de cifras significativas.
2. A la omisión del resto de cifras significativas se le conoce como error de redondeo.
Exactitud y precisión
La precisión se refiere al número de cifras significativas que representan una cantidad y la extensión en las lecturas repetidas de un instrumento que mide alguna propiedad física. La exactitud se refiere a la aproximación de un numero o de una medida al valor verdadero que se supone representa.
La inexactitud (conocida como sesgo) se define como un alejamiento sistemático de la verdad.
Para los dos tipos de errores, la relación entre el resultado exacto o verdadero y el aproximado está dada por:
Valor verdadero = Valor aproximado + Error
Error numérico es igual a la diferencia entre el valor verdadero y el valor aproximado, esto es:
Ev = Valor verdadero – Valor aproximado
Ejemplo:
Supóngase que se tiene que medir la longitud de un puente y de un remache, obteniéndose 9999 y 9 cm, respectivamente. Si los valores verdaderos son 10000 y 10 cm, calcúlese: a) el error y B) el error relativo porcentual de cada caso:
Solución:
a) El error en la medición del puente es de:
Ev = 10 000 – 9 999 = 1 cm
Y para el remache es:
Ev = 10 – 9 = 1 cm
b) El error relativo porcentual para el puente es de:
Ev = 1/ 10 000 100% = 0.01 %
Y para el remache es de:
Ev = 1 / 10 100% = 10%
Por lo tanto aunque ambas medidas tienen un error de 1 cm, el error relativo porcentual del remache es mucho más grande. Se puede concluir que se ha hecho un buen trabajo en la medida del puente, mientras que la estimación para el remache deja mucho que desear.
Error relativo: es el cociente entre el error absoluto y el valor exacto.
Error numérico total
El error numérico total es la suma de los errores de redondeo y de truncamiento. (Los errores de truncamiento decrecen conforme él numero de cálculos aumenta, por lo que se encara el siguiente problema: la estrategia de disminuir un componente del error total lleva al incremento del otro).
Errores por equivocación, de planteamiento o incertidumbre en los datos
En los primeros años de la computación, los resultados numéricos erróneos fueron atribuidos algunas veces al mal funcionamiento de la computadoramisma. Hoy en día, esta fuente de error es muy improbable y la mayor parte de las equivocaciones se pueden atribuir a errores humanos.
Errores de formulación
Los errores de formulación o de modelamiento degeneran en lo que se podría considerar como un modelo matemático incompleto. Un ejemplo de un error de formulación imperceptible es el hacho de que la segunda Ley de Newton no explica los efectos relativisticos.
Incertidumbre en los datos
Algunas veces se introducen errores en un análisis debido a la incertidumbre (sin certeza) de los datos físicos sobre los que se basa el modelo.
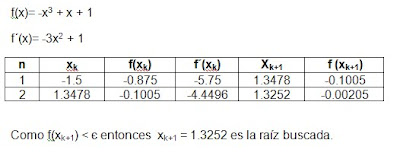
2-1024x145.jpg)