Un método iterativo trata de resolver un problema (como una ecuación o un sistema de ecuaciones) mediante aproximaciones sucesivas a la solución, empezando desde una estimación inicial. Esta aproximación contrasta con los métodos directos, que tratan de resolver el problema de una sola vez (como resolver un sistema de ecuaciones Ax=b encontrando la inversa de la matriz A). Los métodos iterativos son útiles para resolver problemas que involucran un número grande de variables (a veces del orden de millones), donde los métodos directos tendrían un coste prohibitivo incluso con la potencia del mejor computador disponible.
Método de Gauss-Seidel
El método de Gauss-Seidel es un método iterativo y por lo mismo resulta ser bastante eficiente. Se comienza planteando el sistema de ecuaciones con el que se va a trabajar:
De la ecuación 1 despejar x1, de la ecuación 2 despejar x2, …, de la ecuación n despejar xn. Esto da el siguiente conjunto de ecuaciones:
Este último conjunto de ecuaciones son las que forman las fórmulas iterativas con las que se va a estar trabajando. Para comenzar el proceso iterativo, se le da el valor de cero a las variables x2,…, xn; esto dará un primer valor para x1. Más precisamente, se tiene que:
Enseguida, se sustituye este valor de x1 en la ecuación 2, y las variables x3,…, xn siguen teniendo el valor de cero. Esto da el siguiente valor para x2:
Estos últimos valores de x1 y x2, se sustituyen en la ecuación 3, mientras que x4,…, xn siguen teniendo el valor de cero; y así sucesivamente hasta llegar a la última ecuación. Todo este paso arrojará una lista de primeros valores para las incógnitas, la cual conforma el primer paso en el proceso iterativo. Para una mejor comprensión esto se simbolizará de esta forma:
Se vuelve a repetir el proceso, pero ahora sustituyendo estos últimos datos en vez de ceros como al inicio. Se obtendrá una segunda lista de valores para cada una de las incógnitas, lo cual se simbolizará así:
En este momento se pueden calcular los errores aproximados relativos, respecto a cada una de las incógnitas. La lista de errores se presenta a continuación:
El proceso se vuelve a repetir hasta que:
Donde є3 se debe prefijar convenientemente.
Ejemplo: Usar el método de Gauss-Seidel para aproximar la solución del sistema:
hasta que
SOLUCIÓN:
En este caso se puede observar que el sistema no es diagonalmente dominante, lo cual se comprueba con los siguientes cálculos:
Primera fila:
|a11| > (|a12| + |a13|)
5 > (1.4 + 2.7)
5 > 4.1; es cierto.
La condición se cumple para la primera fila.
Segunda fila:
|a22| > (|a21| + |a23|)
2.5 > (0.7 + 15)
2.5 > 15.7; no es cierto.
La condición no se cumple para la segunda fila.
|a33| > (|a31| + |a32|)
4.4 > (3.3 + 11)
4.4 > 14.3; no es cierto.
La condición no se cumple para la tercera fila.
Para que el sistema sea diagonalmente dominante, la condición debe cumplirse para todas las filas. Por lo tanto, el sistema anterior no es diagonalmente dominante.
NOTA: Recuérdese que la diagonal principal está compuesta por a11, a22 y a33.
Sin embargo, al hacer el intercambio del renglón 2 por el renglón 3, se tiene el siguiente sistema:
En este caso se puede observar que el sistema sí es diagonalmente dominante, lo cual se comprueba con los siguientes cálculos:
Primera fila:
|a11| > (|a12| + |a13|)
5 > (1.4 + 2.7)
5 > 4.1; es cierto.
La condición se cumple para la primera fila.
Segunda fila:
|a22| > (|a21| + |a23|)
11 > (3.3 + 4.4)
11 > 7.7; es cierto.
La condición se cumple para la segunda fila.
|a33| > (|a31| + |a32|)
15 > (0.7 + 2.5)
15 > 3.2; es cierto.
La condición se cumple para la tercera fila.
Para que el sistema sea diagonalmente dominante, la condición debe cumplirse para todas las filas. En este caso efectivamente la condición se cumple para todas las filas, por lo cual el sistema anterior es diagonalmente dominante. Por lo tanto se procede a despejar x1, x2 y x3 de las ecuaciones 1, 2 y 3 respectivamente:
Se comienza el proceso iterativo sustituyendo los valores de x2 = 0 x3 = 0 en la ecuación 1 para obtener x1:
x1= -18.84
Ahora se sustituye x1 = -18.84 y x3 = 0 en la ecuación 2 para obtener x2:
x2= -3.152
Por lo tanto los valores obtenidos en la primera iteración son:
x1= -18.84
x2= -3.152
x3= -0.04613
Puesto que sólo se tiene la primera aproximación de la solución del sistema, se debe seguir avanzando en el proceso iterativo. Sustituyendo x2 = -3.152 y x3 = -0.04613 en la ecuación 1, se obtiene x1 = -19.69765; sustituyendo x1 = -19.69765 y x3 = -0.04613 en la ecuación 2, se obtiene x2 = -3.42775; sustituyendo x1 = -19.69765 y x2 = -3.42775 en la ecuación 3, se obtiene x3 = -0.05207. Por lo tanto, la segunda aproximación es:
x1= -19.69765
x2= -3.42775
x3= -0.05207
Ahora se pueden calcular los errores aproximados para cada una de las incógnitas:
Puesto que no se ha cumplido el objetivo, se debe seguir avanzando en el proceso iterativo. Se resumen los resultados de esta manera:
Tercera iteración:
cuarta iteracion:
Así, el objetivo se ha logrado hasta la cuarta iteración y se tiene que los valores aproximados de la solución del sistema son:
x1= -19.77819
x2= -3.45454
x3= -0.05277
2-1024x145.jpg)





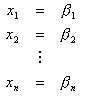









No hay comentarios:
Publicar un comentario